Linear maps, bases and matrices

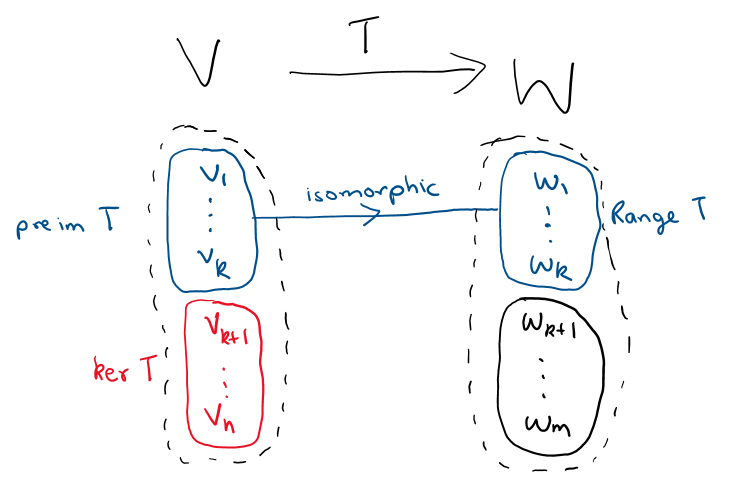
Given vector spaces V and W, we write L(V, W) := the set of all linear maps from V to W. This is a vector space. Some useful properties for a linear map T in L(V, W):

• T injective <=> null(T) = {0}
• null(T) is a subspace of V and range(T) is a subspace of W
• Rank nullity theorem: dim(V) = dim(null(T)) + dim(range(T))
  • Sketch proof: pick a basis u1, …,. um of null(T), extend to basis u1, …, um, v1, …, vn of V. Then T(v1), …, T(vn) is a basis of range(T)

Matrix of a linear map

The matrix M of a linear map T from V –> W, w.r.t a basis v1,…,vn and w1,…,wm is the set of m * n values given by

T(v_i) = M_{1, i} w₁ + … M_{n, i} w_n

A matrix of a linear map is always w.r.t a basis of each of the spaces and we can write M = M (T, (v1, …, vn), (w1, …, wm)) to explicitly show the dependence on the choice of basis.

Can think of the kth column of M as the components (in the w basis) of T applied to the kth basis vector of V

If S : U -> V and T : V -> W and (having chosen bases ui, vi and wi of the three spaces) M(S) and M(T) are the matrices of the linear maps, we have the matrix of the composition map is the product of the matrices M(ST) = M(S) M(T)

With matrix multiplication defined to satisfy the above as : (ST)_{i, j} := Σ_k (S_{i, k} * T_{k, j}) where we dropped the M function for ease of notation

Can think of the jth column of matrix product AB as a linear combination of the columns of A (with the coefficients being the jth column of B).

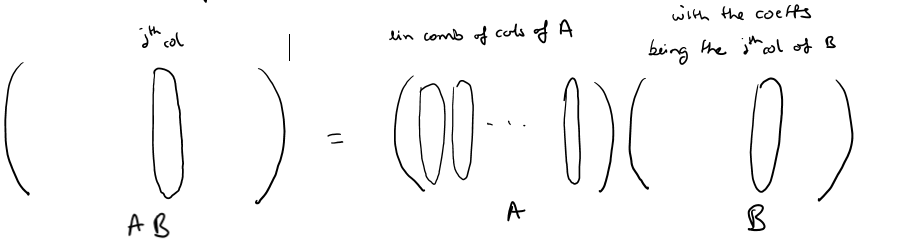
Or can think of the ith row of the matrix product AB as a linear combination of the rows of B (with the coefficients being the ith row of A).

Change of basis

Once you choose a basis for an n-dimensional vector space V, you have an isomorphism between V and Fⁿ via this basis (F = R or C). And thus you can start thinking of elements of v as a list of n numbers

Suppose you have a linear map T : V -> V with a matrix A wrt to a basis u1, …, un of V. You want to find the matrix B wrt a different basis v1, …, vn of V. In the below diagram we have linear maps in blue, isomorphisms via bases to Fⁿ in red and matrix representations of the linear maps in green. First we have the matrix A wrt the basis ui

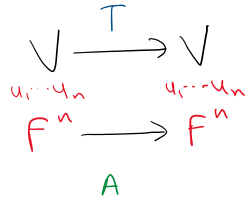
Next we add to this diagram as follows:

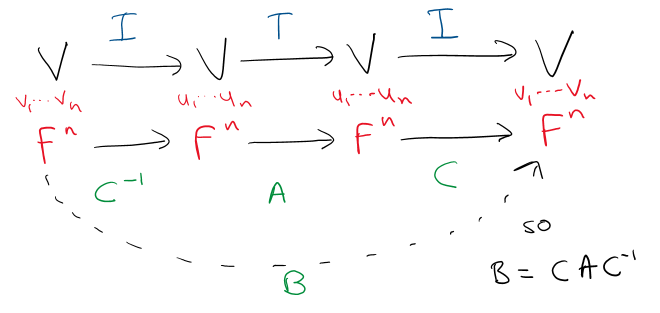
Note we added identity maps to the left and right and hence the overall map from left to right is still T. But now we have the isomorphism to Fⁿ taking place via the new basis vi. C is just the matrix of the identity map from V (with ui basis) to V (with vi basis). Ie the kth column of C is the coefficients when the vector uk is written in the vi bases.